Linkage disequilibrium maps and association mapping

The causal chain between a gene and its effect on disease susceptibility cannot be understood until the effect has been localized in the DNA sequence. Recently, polymorphisms incorporated in the HapMap Project have made linkage disequilibrium (LD) the most powerful tool for localization. The genetics of LD, the maps and databases that it provides, and their use for association mapping, as well as alternative methods for gene localization, are briefly described.

Since its origin a generation ago, genetic epidemiology has dealt with etiology, distribution, and control of disease in groups of relatives and with inherited causes of disease in populations, where inheritance may occur through culture, biology, or interactions between the 2 (1). Advances in molecular genetics have altered the emphasis from family resemblance to identification of genes affecting disease susceptibility, the first step in understanding how the actions of these genes can be ameliorated. At the end of the last century, localization of the gene usually occurred by linkage to a chromosome region within which a random fragment was incorporated, amplified, and then sequenced in a vector such as a bacterial plasmid. This process, called positional cloning (2), evolved into association mapping when the Human Genome Project provided a trustworthy DNA sequence (3) that allowed closely linked polymorphisms to be localized by unique flanking sequences without cloning.

Most of these markers for a short nucleotide sequence are single nucleotide polymorphisms (SNPs), nearly all of which are dichotomous (diallelic). Small insertions and deletions play the same role in mapping as SNPs and are loosely included with them. The number of diallelic markers in the human genome has been estimated to be between 10 and 20 million, depending on exclusion or inclusion of uncommon polymorphisms (4). Detectable association of such polymorphisms with susceptibility to a particular disease (or other phenotype) extends over a much shorter distance than linkage, but the high density of SNPs provides much greater resolution within a candidate region. Because of the short history of association mapping, terminology remains imprecise and is a common source of confusion (see Glossary).

Association between a pair of linked markers is also called linkage disequilibrium (LD) or, less frequently, gametic disequilibrium. However, association has a broader meaning that includes combinations of 3 or more linked markers, at least some of which are in LD. These combinations are called haplotypes if specified for a single chromosome. The sex chromosomes in males and certain chromosomal aberrations are monosomic, with each individual carrying only 1 haplotype. With these exceptions (and some chromosomal aberrations) haplotypes occur in pairs, called diplotypes, consisting of 1 haplotype from each parent. The 2 haplotypes of a diplotype cannot be ascertained with certainty if 2 or more markers are heterozygous except in special cases that include family studies, physical separation of chromosomes, and zero frequency of alternative haplotypes.

This review will focus on methods currently being used for association mapping, but the literature is full of occasional successes by less powerful methods. Association studies have identified many rare, single-gene disorders after localization to a candidate region by linkage or cytogenetic abnormality. Among the first disease gene localizations were cystic fibrosis, Huntington disease, and hemochromatosis. The latter took 16 years because the physical map greatly exceeds the LD map. If the latter had been available, localization could easily have been made in a tenth of the time, with a corresponding reduction in cost. Gene localization in multifactorial inheritance proved more difficult, especially for linkage and cytogenetics, because multiple genes and environmental factors contribute to disease risk, but genes for Alzheimer disease, deep vein thrombosis, inflammatory bowel disease, hypertriglyceridemia, diabetes, schizophrenia, asthma, stroke, myocardial infarction, and a host of other diseases have been identified by association studies. Genome scanning with SNPs has been successful with myocardial infarction, and gene identification is competing with studies of candidate regions. Association studies are expensive, and it is worthwhile to seek the most powerful approaches, even if their language and methods are unfamiliar.

Association mapping depends on the choice of map taken to represent LD. Physical maps specify distance in the DNA sequence, ideally measured in bp. The closest approach to this ideal is by the DNA sequence nominally finished, although errors in many relatively small areas remain and, of course, polymorphisms affecting the DNA sequence are represented by 1 arbitrary allele. For association mapping, it is convenient to represent location in kb to 3 decimal places, retaining full precision in the finished maps. Two physical maps at lower resolution are derived from chromosome breakage in radiation hybrids, the utility of which is limited to organisms without a finished DNA sequence, and chromosome bands that project cytogenetic assignments to the physical map. At all levels of resolution, physical maps have the additivity that defines a linear map. Thus, if the distance in the ith interval between 2 adjacent markers is d_i and if the intervals are mutually exclusive and jointly exhaustive, the distance between any 2 markers is Σd_i, just as in any road map.

Genetic maps also have additivity, but the distance in the ith interval is proportional to ε_id_i, where ε_i is not a constant but an interval-specific scaling factor such that ε_i ≥ 0, and not all ε_i are equal. The distance between any 2 markers if the intervals are mutually exclusive and jointly exhaustive is proportional to Σε_id_i. There are 2 types of genetic maps. Linkage maps long antedated physical maps; their development began in 1913, when Sturtevant (5) elaborated the concept of linear arrangement of genes separated by crossing-over. In 1919, Haldane (6) introduced the Morgan (w) as the length of a chromatid that on average has experienced one crossover event per meiosis, thereby taking w_i = ε_id_i/t as his measurement of distance, where t is the number of generations observed. Until recently, linkage maps have been estimated directly from recombination, since values of ε_i = w_i/d_i could not be determined with accuracy until the physical map was finished. In contrast, LD maps determine distance not from recombination, but from LD, and so distance in the ith interval is expected to be ε_id_i = w_it. The number of generations is large and can be reliably determined only from a population genetics model that allows ε_i to be estimated directly. Whereas haplotype inference from diplotypes complicates association mapping, the 2 types of data provide virtually identical LD maps (7).

In the middle of the last century, population genetics was revolutionized by Gustave Malecot, a professor of applied mathematics at the University of Lyon. His use of probability theory has elucidated evolution, population structure, forensic application of DNA, and LD, where his retrospective approach led others to coalescent theory, which tries to trace current genotypes to a putative ancestor. These contributions were summarized several years after his death (8) and continue to stimulate population genetics. The basic theory for LD assumes a pair of diallelic loci that underwent a population bottleneck of reduced size because of war, famine, epidemic, migration, or other factors. Let the founder haplotype frequencies be a mixture of extreme LD with probability ρ₀ and a complementary frequency with LD = 0:

Probability1

The frequency of the rarest allele is Q, and R is the frequency of the associated allele. Then ρ₀ is defined as the association probability in founders, and the expected decay of ρ in t generations gives ρ_t = (1 – L)Me^–θt + L where M = (ρ₀ – L)e^{(v + 1/2N)t}/(1 – L) and v, N, and L are the mutation rate, effective population size, and asymptotic value of ρ_t as e^–θt & rarr; 0, respectively (9). Random variation including later bottlenecks causes departure from this expectation, but attempts to anticipate its effects are unsuccessful because the ancestral frequencies and the values of v, N, and t are unknown.

The history of this Malecot equation has been reviewed (10). The value of t is so large that excess of ρ_t over L is usually negligible unless recombination θ is so small that 2 or more crossovers in the same small region are almost always separated by generation and therefore independent. Then the Haldane mapping function is appropriate, with θ = (1 – e^–2w)/2 & rarr; w and wt = Σε_id_i. Therefore the resolution of linkage maps can be enhanced by interpolating dense locations from LD maps, and (more importantly) association mapping can be based on LD maps that have additive distances measured by Σε, with Σε_id_i= 1 defining 1 LD unit (LDU). The effective bottleneck time in generations is therefore the ratio of LDU to the corresponding distance on the sex-average linkage map in Morgans.

There is an infinity of metrics that describe association for pairs of diallelic markers or affection by marker in a 2 × 2 table. Designating an arbitrary metric by ψ with information K_ψ under the null hypothesis that ψ = 0, all of these metrics have the property that in large-sample theory χ²₁ = ψ²K_ψ. Tests on pairs of associated markers are not independent, but n tests give a composite likelihood (lk) with –2lnlk = Σ_iK_ψi (_I – ψ_i)² and variance V = –2lnlk/(n – m) under a hypothesis with m parameters estimated. This does not have the precision of true likelihood, but it gives a good estimate of relative efficiency V/V′ of an alternative hypothesis with the same data, but a greater variance V′. This is one of several ways to compare different approaches to LD maps and association mapping.

The initial impetus for LD maps came from the discovery that the association probability ρ is predicted by the Malecot equation and provides a higher relative efficiency than other metrics that describe association for pairs of diallelic loci (9, 11). This early research antedated the physical map, the first (“finished”) version of which was preceded by evidence from small sequences, that LD is expressed as alternating regions of high and low disequilibrium (blocks and steps) that are fairly stable among populations and are therefore ascribed to low and high recombination, respectively. An ingenious technique for typing recombination in large numbers of sperm has confirmed that ascription in 1 sequence (12), but the method is currently too laborious for use with whole chromosomes. Figure 1 shows how closely the LD map (portrayed here not as coordinates but as a graph) corresponds with recombination. The idea arose that blocks and steps might be so precisely defined that they could be the basis for maps of haplotypes in single blocks delimited by flanking steps. Unfortunately, the frequencies of sequences punctuated in this way varies from 0.02 to 0.40, making haplotype delimitation both arbitrary (13) and acutely sensitive to SNP density (14). These preliminary results led to LD maps delimited in LDU by estimation of the ε_i simultaneously with the Malecot parameters (7). These LD maps were shown to have a much higher relative efficiency than the kb map, both in describing LD (15) and in association mapping (16). The age of a diallelic polymorphism has been shown to be correlated with its minor allele frequency (17), but time t since the last major bottleneck follows a different pattern with constancy except for alleles that were rare at the last bottleneck or have arisen since (18). Estimates of t are about 1,500 generations in Eurasians and greater in Africans, but this is less than the conventional time assigned to migration out of Africa. Perhaps later bottlenecks tended to reverse progress toward equilibrium, or uncommon alleles tended to be restricted to a few isolates with consequent reduction in effective population size.

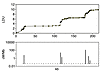Figure 1

Graph of an LD map for a 216-kb segment of class II region of MHC (7) with corresponding recombination hotspots (12).

One of the attractive features of an LD map is that it can evolve with high relative efficiency from low to high density, from a simple to a more complex model, or from a cosmopolitan map based on several populations to a map specific for a given population, just by beginning iterative estimation with the ε_i of the preliminary map. This convenience may be exploited in a location database to obtain LD maps more specific and more accurate than the contents of the database. In principle, linkage maps could be developed in the same way if the computer programs for linkage mapping accepted trial values for marker locations instead of merely marker order.

Association mapping localizes genes affecting disease susceptibility or other phenotypes through association with nearby polymorphisms, usually SNPs. Often association mapping is oriented by previous low-resolution linkage mapping with multiallelic markers to a chromosomal region that is too large for identification of the causal locus, but falling costs of SNP typing have made whole genome scans feasible even for linkage, and the lesser power of single SNPs is compensated for by their much greater density and lower typing costs than multiallelic markers. Successful association mapping at high density leads to causal SNPs that may be confirmed by functional assays with allowance for association. This classical problem of discriminating causality from correlation, the highest level of epidemiology and other nonexperimental sciences, is common to association and functional tests. Zhang et al. (19) described 4 stages from linkage to function during which the search region shrinks and SNP density approaches saturation.

The rigor with which typing and analysis should be carried out has discouraged some scientists (20), but the goal is potentially precious and much has been achieved. Half a century ago, linkage showed that clinically inseparable types of elliptocytosis are determined by different genes (21). This stimulated linkage studies that have shown unanticipated diversity, with at least 8 loci for recessive limb girdle muscular dystrophy instead of the single locus that was once disputed and hundreds of loci for mental retardation and profound deafness and blindness. The immediate impact has been diagnostic for genetic counselling and in some cases for specific treatment. The long-term goal is to develop human genetics to the point where the function and dysfunction of every gene is well understood and to develop pharmacogenetics to the point where every gene for disease susceptibility has a maximally efficient treatment with minimal side effects. Obviously this goal has not been reached only 2 years after substantial completeness of the Human Genome Project made an LD map possible.

A serious obstacle to association mapping is the inverse relation between allele frequency and effect modeled by exponential risk (Figure 2) (22). The major genes of large effect that are the basis of classical genetics are mostly rare. Polygenes of extremely small effect on fitness account for nearly all alleles subject to selection and are currently beyond cost-effective study. Between them are oligogenes with effects large enough to be detected in a feasible study and perhaps elucidate clinically important metabolic patterns or even be useful targets for pharmacogenetics.

Figure 2

Allele frequency by effect.

Whereas Figure 1 deals only with alleles subject to selection, the much larger number of neutral polymorphisms has a nearly uniform distribution, with an excess of small frequencies arising from mutation during population expansion since the Pleistocene era. It is currently inconceivable that a genome scan could be based on enough polymorphisms to ensure inclusion of a particular causal SNP, although selection of nonsynonymous substitutions that alter an amino acid would to some extent increase the inclusion probability (4) whereas attempts to reduce the number of SNPs by selection to conserve diversity reduces power (19). Several papers advocate pooling DNA from several individuals for association mapping, but so far the technique has been too delicate to compete with pooling single samples (23).

Most association mapping with an LD map has used composite likelihood for single SNPs, replacing d_i with δ_i (S_i–S_D), where S_i is the location on the LD map of the ith SNP, S is the location of a putative causal SNP, and δ_i is the Kronecker δ that takes the value 1 if S_i ≥ S and –1 otherwise, thereby assuring that the derivative of the composite likelihood takes the appropriate sign. Experience has shown that estimates of L and ε are seldom significantly better than for the LD map, and so iteration is often limited to M and S. Good results have been obtained with real and simulated data (16). So far, the association probability ρ has been limited to dichotomous traits but can be extended to quantitative traits.

It is possible to apply an LD map to haplotypes, which may well model the frequency of a causal SNP more accurately than a neighboring associated SNP. Among the problems to be overcome are estimation of haplotype probabilities for each diplotype, perhaps including inference (imputation) of untyped SNPs. Imputation introduces error while failure to impute discards a proportion of participants that increases with the number of SNPs in a haplotype, which also governs the number of haplotypes to be tested. The optimal number of SNPs in a haploset defined by a given set of SNPs appears to be small but must depend on their density and the LD map. The simplest haploset for association mapping is of size 2 with the causal SNP intermediate on the LD map. The most significant haplotype is identified by the same logic as multiple alleles (11). This design is unique in that overlapping windows do not overlap intervals (e.g., SNP pairs 1,2 and 2,3 do not overlap). Haplotypes with an even number of SNPs take the LD location of the midpoint of their median pair whereas haplosets with an odd number of SNPs take the LD location of their medial SNP. Windows of 3 or more SNPs overlap, generating progressively higher autocorrelations as the number of SNPs increases. These problems have not been solved, but research on association mapping with haplotypes and an LD map is being actively pursued.

Association mapping is possible without an LD map, most simply by selecting the most significant single SNP or haploset. This avoids composite likelihood at the high cost of losing all information about other markers, dispensing with a support interval, and accepting a heavy correction that is prohibitive in a genome scan (24). Neglecting approaches that have not been applied since the physical map was nominally finished, mathematicians have proposed 3 alternatives to LD maps, all using haplotypes. One is non-Bayesian and uses logistic regression based on a similarity graph to select the most significant haploset with an appropriate correction (25). Since only 1 point is specified, the kb and LD maps provide identical results. Comparison with methods that provide a support interval and relative efficiency is not possible.

The other 2 methods are at once coalescent, Bayesian, and haplotypic. Coalescent theory assumes equilibrium, sacrificing an estimate of time (t) that is the principal discriminant between sex-averaged linkage and LD. Interpolation into one of these maps is necessary if the coalescent is to be used for linkage or association mapping, ignoring concern that coalescent theory provides “estimates of the recombination rate from polymorphism data [that] are extremely unreliable” (26). Bayesian methods use prior probabilities based on evidence in the sample and are therefore posterior probabilities, making the number of degrees of freedom unclear and residual variance ambiguous. It is difficult to compare results with non-Bayesian LD maps based on a defined set of parameters estimated without preconceptions. Objective criteria for this comparison must be sought, although in other applications the conflict between a few mathematicians who use Bayesian models and most scientists who reject them remains dogmatic. However these issues are resolved, the utility of efforts to improve construction of LD maps or find a more efficient substitute for association mapping should be measured in 4 ways: (a) correspondence with the sex-averaged linkage map; (b) residual variance of alternative LD maps; (c) capability of identifying systematic departures from the scaled linkage map due to selection and other evolutionary events; and (d) power for association mapping. So far, only composite likelihood on LD maps provides all these data and therefore yields a benchmark against which alternatives may be measured. One Bayesian method has a much larger support interval and estimation of error than association mapping with an LD map in the single example for which both were tried (27, 28). The other Bayesian example was scaled to a linkage map but has not yet been applied to an LD map or association mapping (29).

During the last century, genetic information was obtained for Drosophila melanogaster, Mus musculus, and Homo sapiens. Drosophila led the way by giving each identified locus its position on the linkage map and assignment to a band on a salivary chromosome (30). The human map developed after isozymes and somatic cell hybrids supplied a substantial number of markers (31). As the number of map loci increased, the workshops in which maps were updated became chromosome-specific and then were abandoned in favor of computer databases that initially focused on linkage (32), now extended to physical location and LD. At present, the minimal location database (33) has an entry for each point (SNP, expressed locus, microsatellite, insertions and deletions, etc.), the locus if assigned therein, the chromosome band assignment, kb location, location in cM in the male and female linkage maps, location in one or more LD maps, and minor allele frequency (Table 1). Such a location database allows replacement of kb location as the “finished” map is refined, updating of location in the LD map(s), interpolation from LD to linkage maps, and use of a standard LD map to give starting values for a local map at higher density or for interpolation from such a local map into the standard map. Discrepancies between linkage and LD maps can be detected and effort made to explain them. The utility of a location database is so great that in time it may be adopted by national and international centers of bioinformatics. Perhaps even the forgettably long accession numbers of SNPs will be replaced by a more informative nomenclature.

Table 1

An abbreviated location database

The short history of LD maps and association mapping leaves many questions unanswered. LD maps were first applied to small regions at moderate density, using a single algorithm. Extension to whole chromosomes introduces computational problems that can be addressed in many ways, and LD maps can be created faster and more reliably than by methods now in use to create them. Relative efficiency to describe linkage and LD is critical, but other measures of reliability will be developed.

Association mapping raises different problems. An LD map obviously excels the kb map for SNP assignment to a block, but within a block, all SNPs have the same location in LDU. Slight inclination of a critical block improves association mapping, but the best algorithm has not been established, and the most effective use of haplotypes has not been determined. Association mapping shares with LD maps the problem of recognizing and discarding inferior methods, but the evidence from support intervals and location error is clearly different from reliability measures for LD maps.

The utility of a location database can be enhanced if LD maps are progressively improved rather than beginning each update with the kb map. Operations on the database should allow interpolating high resolution LD into linkage maps without confounding the 2 sources of information. The challenge is 2-fold: first to geneticists, who must identify the most useful contents and operations for local databases; and second, to large centers, such as the European Bioinformatics Institute and the National Centre for Biotechnology Information, which must recognize that the problem is numerical rather than pictorial. Unless it is solved, the Human Genome Project will not realize its potential.

LD maps and association mapping are separated by 90 years from the development of linkage, and their applications are just beginning. Peripheral details and controversial enterprises such as selection of tagging SNPs and definition of blocks should not distract us from the central aim: to fulfill the promise of LD maps and association mapping in medicine, molecular biology, and the understanding of evolution.

View Glossary

The contribution of the University of Southampton to the research reported herein was supported in part by grants from the United Kingdom Medical Research Council and Applied Biosystems.

Nonstandard abbreviations used: LD, linkage disequilibrium; LDU, LD unit; SNP, single nucleotide polymorphism.

Conflict of interest: The author has declared that no conflict of interest exists.

1. Morton, N.E., and Chung, C.S. 1978. Preface. In Genetic epidemiology. N.E. Morton and C.S. Chung, editors. Academic Press. New York, New York, USA. IX–X.
2. Collins, FS. Positional cloning: let’s not call it reverse anymore. Nat. Genet. 1992. 1:3-6.
   View this article via: PubMed CrossRef Google Scholar
3. Abramowicz, M. The Human Genome Project in retrospect. Adv. Genet. 2003. 50:231-261, discussion 507–510.
   View this article via: PubMed CrossRef Google Scholar
4. Botstein, D, Risch, N. Discovering genotypes underlying human phenotypes: past success for Mendalian disease, future approaches for complex disease. Nat. Genet. 2003. 33(Suppl.):228-237.
   View this article via: PubMed CrossRef Google Scholar
5. Sturtevant, AH. The linear arrangement of six sex-linked factors in Drosophila, as shown by their mode of association. J. Exp. Zool. 1913. 14:43-59.
   View this article via: CrossRef Google Scholar
6. Haldane, JBS. The combination of linkage values, and the calculation of distances between the loci of linked factors. J. Genet. 1919. 8:299-309.
7. Maniatis, N, et al. The first linkage disequilibrium (LD) maps: delineation of hot and cold blocks by diplotype analysis. Proc. Natl. Acad. Sci. U. S. A. 2002. 99:2228-2233.
   View this article via: PubMed CrossRef Google Scholar
8. Slatkin, M., and Veuille, M. 2002. Modern developments in theoretical population genetics. The legacy of Gustave Malecot. Oxford University Press. Oxford, United Kingdom/New York, New York, USA. 280 pp.
9. Morton, NE, et al. The optimal measure of allelic association. Proc. Natl. Acad. Sci. U. S. A. 2001. 98:5217-5221.
   View this article via: PubMed CrossRef Google Scholar
10. Morton, N.E. 2002. Applications and extensions of Malecot’s work in human genetics. In Modern developments in theoretical population genetics. M. Slatkin and M. Veuille, editors. Oxford University Press. Oxford, United Kingdom. 20–36.
11. Collins, A, Morton, NE. Mapping a disease locus by allelic association. Proc. Natl. Acad. Sci. U. S. A. 1998. 95:1741-1745.
    View this article via: PubMed CrossRef Google Scholar
12. Jeffreys, AJ, Kauppi, L, Neumann, R. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 2002. 29:217-222.
13. Daly, MJ, Rioux, JD, Schaffner, SF, Hudson, TJ, Lander, ES. High-resolution haplotype structure in the human genome. Nat. Genet. 2001. 29:229-232.
    View this article via: PubMed CrossRef Google Scholar
14. Ke, X, et al. The impact of SNP density on fine-scale patterns of linkage disequilibrium. Hum. Mol. Genet. 2004. 13:577-588.
    View this article via: PubMed CrossRef Google Scholar
15. Zhang, W, Collins, A, Maniatis, N, Tapper, W, Morton, NE. Properties of linkage disequilibrium (LD) maps. Proc. Natl. Acad. Sci. U. S. A. 2002. 99:17004-17007.
    View this article via: PubMed CrossRef Google Scholar
16. Maniatis, N, et al. Positional cloning by linkage disequilibrium. Am. J. Hum. Genet. 2004. 74:846-855.
    View this article via: PubMed CrossRef Google Scholar
17. Kimura, M, Ohta, T. The age of a neutral mutant persisting in a finite population. Genetics. 1973. 75:199-212.
    View this article via: PubMed Google Scholar
18. Zhang, W, et al. Impact of population structure, effective bottleneck time, and allele frequency on linkage disequilibrium maps. Proc. Natl. Acad. Sci. U. S. A. 2004. 101:18075-18080.
    View this article via: PubMed CrossRef Google Scholar
19. Zhang, W, Collins, A, Morton, NE. Does haplotype diversity predict power for association mapping of disease susceptibility? Hum. Genet. 2004. 15:157-164.
20. Couzin, J. New mapping project splits the community. Science. 2002. 296:1391-1393.
    View this article via: PubMed CrossRef Google Scholar
21. Morton, NE. The detection and estimation of linkage between the genes for elliptocytosis and the Rh blood type. Am. J. Hum. Genet. 1956. 8:80-96.
    View this article via: PubMed Google Scholar
22. Morton, NE. Significance levels in complex inheritance. Am. J. Hum. Genet. 1998. 62:690-697.
    View this article via: PubMed CrossRef Google Scholar
23. Godde, R, et al. Refining the results of a whole-genome screen based on 4666 microsatellite markers for defining predisposition factors for multiple sclerosis. Electrophoresis. 2004. 25:2212-2218.
    View this article via: PubMed CrossRef Google Scholar
24. Risch, N, Merikangas, K. The future of genetic studies of complex human diseases. Science. 1996. 273:1516-1517.
    View this article via: PubMed CrossRef Google Scholar
25. Durrant, C, et al. Linkage disequilibrium mapping via cladistic analyses of single-nucleotide polymorphism haplotypes. Am. J. Hum. Genet. 2004. 75:35-43.
    View this article via: PubMed CrossRef Google Scholar
26. Nordborg, M. 2001. Coalescent theory. In Handbook of statisticalgenetics. D.J. Balding, M. Bishop, and C. Cannings, editors. John Willey & Sons, Ltd. Chichester, United Kingdom. 179–212.
27. Morris, AP, Whittaker, JC, Xu, CF, Hosking, LK, Balding, DJ. Multipoint linkage-disequilibrium mapping narrows location interval and identifies mutation heterogeneity. Proc. Natl. Acad. Sci. U. S. A. 2003. 100:13442-13446.
    View this article via: PubMed CrossRef Google Scholar
28. Maniatis, N, et al. The optimal measure of linkage disequilibrium minimizes error in association mapping of affection status. Hum. Mol. Genet. 2005. 14:187-195.
29. McVean, GA, et al. The fine-scale structure of recombination rate variance in the human genome. Science. 2004. 304:581-584.
    View this article via: PubMed CrossRef Google Scholar
30. Bridges, C.B., and Brehme, K.S. 1944. The mutants of drosophila melangaster. Carnegie Institution of Washington Publications. Washington, DC, USA. 552 pp.
31. D. Bergsma, editor. 1974. Human gene mapping. Vol. X, issue 3 of Birth defects original article series. The National Foundation, March of Dimes. Intercontinental Medical Book Corporation. New York, New York, USA. 216 pp.
32. Collins, A, Frezal, J, Teague, J, Morton, NE. A metric map of humans: 23,500 loci in 850 bands. Proc. Natl. Acad. Sci. U. S. A. 1996. 93:14771-14775.
    View this article via: PubMed CrossRef Google Scholar
33. Ke, X, Tapper, W, Collins, A. LDB2000: sequence-based integrated maps of the human genome. Bioinformatics. 2001. 17:581-586.
    View this article via: PubMed CrossRef Google Scholar